Sangaku of San Gaku (算額: wiskundige tablet) zijn Japanse puzzels in de Euclidische meetkunde
gemaakt door leden van alle sociale klassen op houten tafels gedurende de Edoperiode (1603-1867).
Een typisch probleem, gepresenteerd op een tafel uit 1824 in de prefectuur Gunma,
gaat over de relatie tussen drie elkaar rakende cirkels met een gemeenschappelijke raaklijn.
Gegeven de straal van de twee buitenste grote cirkels, wat is de straal van de kleinste in het midden?
Het antwoord (met bewijs) lees je hieronder.

Enkele jaren geleden ontving ik van de redactie
van het Nederlandse tijdschrift Pythagoras
een mok waarop een sangaku staat afgebeeld.
EIGENSCHAP
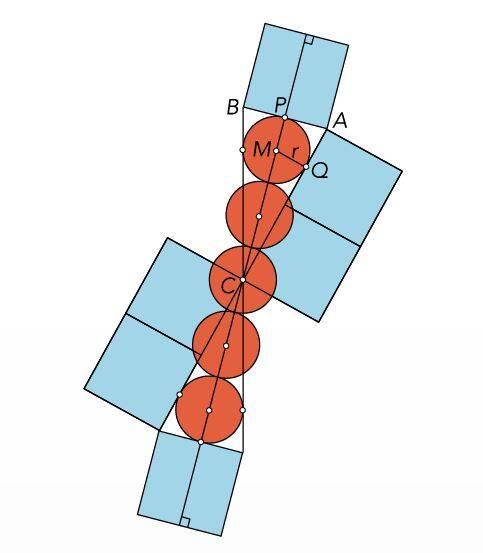
Driehoek ABC (waarbij |AC| = 2 .|AB|) en zijn spiegelbeeld t.o.v. het hoekpunt C vormen een 'zandloperfiguur'.
De ingeschreven cirkel van driehoek ABC heeft straal r.
Dan passen 5 dergelijke cirkels in de zandloper.
Een bewijs (van een algemenere vorm van deze eigenschap) staat naast de figuur hieronder.
Bron: tijdschrift Pythagoras - september 2008.

Ik voeg hier graag een eigen sangaku aan toe.
Via het document in bijlage kan je meegenieten van 27 sangaku's
die Jens Bossaert voor ons verzamelde.
Hij geeft je meteen bij elke sangaku ook een tip voor het bewijs.
Maak jouw eigen website met JouwWeb