Claudius Ptolemaeus (ca. 87 - 150, Alexandrië)
gebruikte de wiskunde als hulpmiddel voor berekeningen in de astronomie.
In zijn boek Almagest geeft hij een samenvatting van de toenmalige kennis
over de astronomie en stelt hij koordentabellen op
waarmee hij afstanden berekent tussen punten op een cirkel.
In zijn werk vinden we ook enkele merkwaardige en originele stellingen terug
uit de meetkunde en de goniometrie.
Hieronder geven we het klassieke bewijs voor de stelling van Ptolemaeus voor een koordenvierhoek.
We voegen er ook een 'bewijs zonder woorden' aan toe (Bron: www.cut-the-knot.org).
Daarna volgt een schets van een bewijs met behulp van de cosinusregel.
Tenslotte komt nog een leuke opgave aan bod waarin pi opduikt
en een verrassende toepassing via de omgeschreven cirkel van een gelijkzijdige driehoek.
Een 'bewijs zonder woorden'.
Een bewijs met behulp van de cosinusregel.
TE BEWIJZEN: ac + bd = mn
Voor het bewijs volstaat het 4 keer de cosinusregel toe te passen:
op Δ ABD en Δ BCD waarbij ∠ BAD en ∠ DCB supplementaire hoeken zijn
en op Δ ABC en Δ CDA waarbij ∠ ABC en ∠ CDA supplementaire hoeken zijn.
En supplementaire hoeken hebben een tegengestelde cosinuswaarde
Door hieruit telkens de cosinussen te elimineren
vind je uiteindelijk (reken maar eens na!) dat
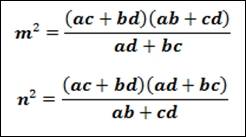
Door deze uitdrukkingen tenslotte lid-aan-lid met elkaar te vermenigvuldigen, bekom je de gewenste formule.
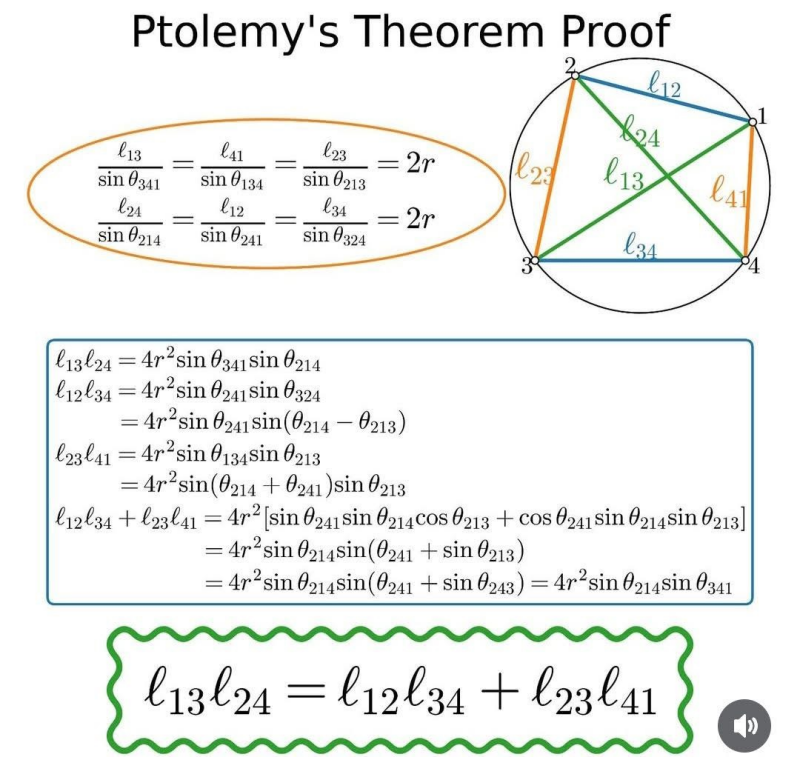
Een van de mooiste stellingen uit de vlakke euclidische meetkunde wordt bewezen met behulp van de stelling van Ptolemaeus.
Aan Brahmagupta wordt nog een ander merkwaardig resultaat voor een koordenvierhoek toegeschreven.
Die stelling ontdek je hieronder.
Maak jouw eigen website met JouwWeb